Open Source Math Texts at the 2014 JMM

There are going to be sessions on open source math texts at the 2014 Joint Math Meetings in Baltimore January 15-18.   The sessions are on Friday January 17 , 8-10:55 and 3-4:55.  I'm speaking on our  text, Applied Discrete Structures.  Because of a family obligation, I requested a late time, and I got the last time slot in the afternoon session, at 4:40.   My Title is "What a Difference 30 Years Makes!  -Adventures in Mathematics Textbook Publishing."   The sessions will be in Room 349 of the Baltimore Convention Center.

I'd love to meet up with anyone who has been using our book!

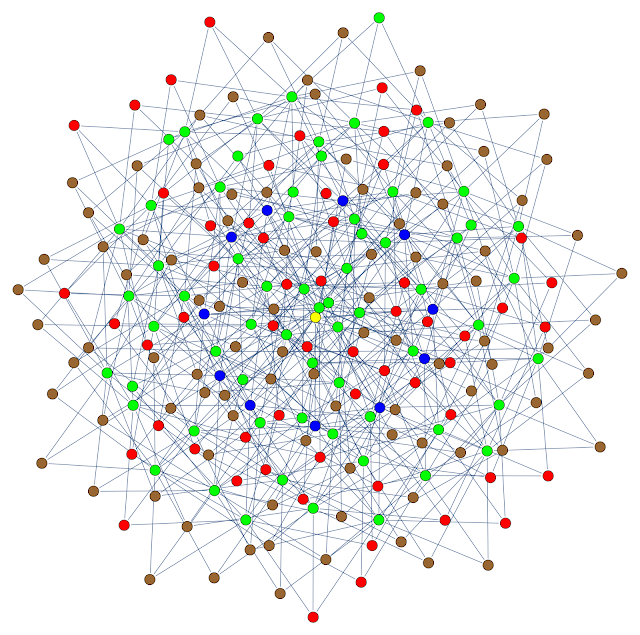
A sphere in binary 11-space

In my discrete math class this week, did an example of a code that encodes three bits to eleven bits and can correct all two-bit errors.   This particular code was not meant to be particularly optimal, but for one particular example I ran with 3,000,000 bits, the number of errors was roughly 1/4 of what was predicted by the probabilities, given that two bit errors can be corrected.  There were 38 failures instead of a predicted 155.   This is no mystery since the packing of spheres in {0,1}^11 wasn't expected to be all that tight, and three bit errors can often be corrected.  

The encoding function is 

         (a, b, c) ----> (a, b, c, a + b, a + c, b + c, a + b + c, a + b, a + c, b + c, a + b + c)

To get an visualize the situation, I create the graph below.   The vertices are some of the points in the code space: the sphere of radius three centered around one of the code words.   The color coding is

• Yellow:   the code word - I used the zero word, but the space is symmetric everywhere.
• Blue:   points one unit from the code word
• Green:  points two units from the code word
• Brown:  points three units from the code word and further that three units from all other code words.
• Red:  points three units from the code word but also three units from another code word.

So all but the Red points, if received, will correct to the most likely transmitted word.   Only the Red ones are questionable and there is no most likely correction.

The Economic Impact of Applied Discrete Structures.

I've been starting to collect data to document the economic impact of Applied Discrete Structures.  In a class using our text, the cost to a student ranges from $0, if  he/she uses the pdf, to $30 a hard copy of purchased.   A rough estimate of the percentage students that buy a hard copy is 15%.   Prior to using our text at UMass Lowell, we used a text that cost $160 new, and around $120 used.   So a very conservative estimate of the impact on student costs would be $120 times the number of students enrolled in discrete math classes using our book.  Here are the estimated student savings, also with very conservative estimates for enrollments starting Fall 2011 through the Spring 2013 semester:

UMass Lowell:   300 students have saved a collective $36,000

Other Colleges:   75  students have saved a collective $9,000

That's $45,000 that students have saved in the first couple of years that the book has been available.   We're hoping that with increased exposure on open source textbook websites, we can dramatically increase the impact outside of UMass Lowell.

So far we are listed on the following sites:

• Merlot Open Textbook Services
• University of Minnesota Open Textbook Catalog
• The American Institute of Mathematics 
• U. of Puget Sound Open Content Math Curriculum
• collegeopentextbooks.org

Version 2.0 is now available

Version 2.0 of Applied Discrete Structures is now available both in pdf form and printed, from lulu.com.

Here are a few notes on the new version:
•  The full version is now 494 pages, with two blank pages added for the lulu version.
•  The pdf's are still absolutely free!
•  The prices of the full printed version and Part 2 (Chapters 11-16) are the same as before.  The price of Part 1 (Chapters 1-10) has dropped by $1.
•  The most significant change in content is in the chapter on Relations, which has been reorganized.  It's logical flow is a bit smoother now, thanks to suggestions from Dan Klain.  Other chapters where a few alterations have been made:  Chapters 10 and 13.
•  The pdf's now have links to the first page in each chapter in the table of contents.


For pdf copies:   http://faculty.uml.edu/klevasseur/ads2/
For printed copied:  lulu.com

Applied Discrete Structures: a three year status report

The impetus for Applied Discrete Structure was my attendance at a Sage Day at the Clay Math Institute in December 2009.   Al Doerr and I got our copyright back from Pearson a few months after that and so we are just about three years into this project.

Probably the most important milestone was March of last year, when we assembled a complete version of the book and made it available for free on our web site and also for a reasonable price ($30) on lulu.com.

In the past year there have been two other milestones:

• We are now listed on the American Math Institute's Open Textbook Initiative site.
• We have several outside adoptions: classes at the University of the Puget Sound, Grinnell College, Casper College and Luzurne Community College are all using our book.

March seems to be a good time to update the book in anticipation of fall adoptions, so I've been working V2 of the full pdf.  It's really just about ready, but I'm going to allow a bit more time pick up more errata from V1.  Particular thanks to students at Luzurne CC, who have found several typos.