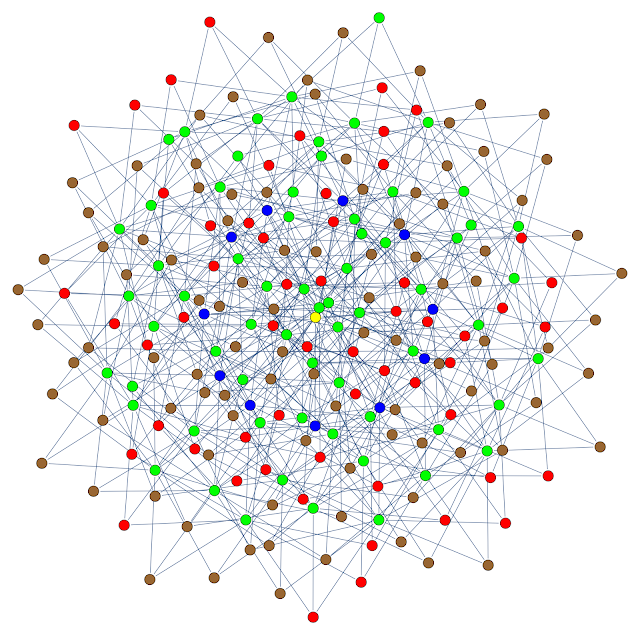
A sphere in binary 11-space
In my discrete math class this week, did an example of a code that encodes three bits to eleven bits and can correct all two-bit errors. This particular code was not meant to be particularly optimal, but for one particular example I ran with 3,000,000 bits, the number of errors was roughly 1/4 of what was predicted by the probabilities, given that two bit errors can be corrected. There were 38 failures instead of a predicted 155. This is no mystery since the packing of spheres in {0,1}^11 wasn't expected to be all that tight, and three bit errors can often be corrected.
The encoding function is
(a, b, c) ----> (a, b, c, a + b, a + c, b + c, a + b + c, a + b, a + c, b + c, a + b + c)
To get an visualize the situation, I create the graph below. The vertices are some of the points in the code space: the sphere of radius three centered around one of the code words. The color coding is
- Yellow: the code word - I used the zero word, but the space is symmetric everywhere.
- Blue: points one unit from the code word
- Green: points two units from the code word
- Brown: points three units from the code word and further that three units from all other code words.
- Red: points three units from the code word but also three units from another code word.
So all but the Red points, if received, will correct to the most likely transmitted word. Only the Red ones are questionable and there is no most likely correction.
